[GIS算法] 2.4.1 判断两线段是否相交 – C语言实现
目录
判断两线段是否相交
- 线段P1P2
- 线段Q1Q2
算法一:快速排斥+跨立试验
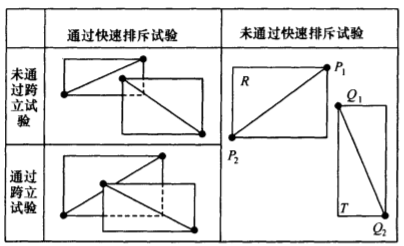

快速排斥试验
- 以线段P1P2为对角线的矩形R
- 以线段Q1Q2为对角线的矩形T
【思路】如果R和T不相交 => 两线段也不相交。但是否相交,还需要第二步的判断:跨立试验
跨立试验
【思路】如果两线段相交,则两线段必然相互跨立对方
【判断依据】
- P1P2跨立Q1Q2: (P1-Q1)×(Q2-Q1)×(Q2-Q1)×(P2-Q1)≥0
- Q1Q2跨立P1P2: (Q1-P1)×(P2-P1)×(P2-P1)×(Q2-P1)≥0
【推算】P1P2跨立Q1Q2 => 矢量(P1-Q1)和(P2-Q1) 位于 矢量(Q2-Q1) 的两侧 => (P1-Q1)×(Q2-Q1)×(P2-Q1)×(Q2-Q1)<0 => (P1-Q1)×(Q2-Q1)×(Q2-Q1)×(P2-Q1)<0
【思考】
- (P1-Q1)×(Q2-Q1)=0 => (P1-Q1)和(Q2-Q1)共线 => 但已通过快速排斥试验 => P1一定在线段Q1Q2上
- 同理,(Q2-Q1)×(P2-Q1)=0 => P2一定在Q1Q2上
代码
typedef struct vector{
double x,y;
}Vector; //向量
typedef struct{
double xmax,xmin;
double ymax,ymin;
}MBR;
/*
* 由两个点构造一个向量
*/
Vector VectorConstruct(Point A, Point B) {
Vector v;
v.x = B.x - A.x;
v.y = B.y - A.y;
return v;
}
// 向量的叉积
double CrossProduct(Vector a, Vector b) {
return a.x * b.y - a.y * b.x;
}
/*
* 由两个点构造一个MBR
*/
MBR MbrConstruct(Point A, Point B) {
MBR m;
if (A.x > B.x) {
m.xmax = A.x;
m.xmin = B.x;
}
else {
m.xmax = B.x;
m.xmin = A.x;
}
if (A.y > B.y) {
m.ymax = A.y;
m.ymin = B.y;
} else
{
m.ymax = B.y;
m.ymin = A.y;
}
return m;
}
/*
* 判断两个MBR是否有交集,有返回1,否0
*/
int MbrOverlap(MBR m1, MBR m2) {
double xmin, xmax, ymin, ymax;
xmin = Max(m1.xmin, m2.xmin);
xmax = Min(m1.xmax, m2.xmax);
ymin = Max(m1.ymin, m2.ymin);
ymax = Min(m1.ymax, m2.ymax);
return (xmax >= xmin && ymax >= ymin) ? 1 : 0;
}
/*
* 判断两线段(线段AB和CD)是否相交,是返回1,否0
* 快速排斥+跨立
*/
int SegmentIntersection(Point A, Point B, Point C, Point D) {
// (1)判断AB和CD所在的MBR是否相交
MBR m1 = MbrConstruct(A, B);
MBR m2 = MbrConstruct(C, D);
if (MbrOverlap(m1, m2) == 0)
return 0;
// (2)跨立判断
Vector CA = VectorConstruct(C, A);
Vector CB = VectorConstruct(C, B);
Vector CD = VectorConstruct(C, D);
Vector AC = VectorConstruct(A, C);
Vector AD = VectorConstruct(A, D);
Vector AB = VectorConstruct(A, B);
// AB跨立CD,并且,CD跨立AB
if (CrossProduct(CD, CA) * CrossProduct(CD, CB) <= 0 && CrossProduct(AC, AB) * CrossProduct(AD, AB) <= 0)
return 1;
else
return 0;
}
算法二:参数方程求解
线段AB、线段CD是否相交
【定义】线段的参数方程:
- AD = A + r(b-A),r∈[0,1] (用r描述AB线段上的每个点,不再是x,y)
- CD = C + s(D-c),s∈[0,1]
【推算】Ax,Ay表示A的横坐标、纵坐标
如果AB、CD相交 => A+r(B-A)=C+s(D-c) => Ax+r(Bx-Ax)=Cx+s(Dx-Cx),Ay+r(By-Ay)=Cy+s(Dy-Cy), r、s∈[0,1] => 解方程,得到r,s

【判断方法】设P为AB、CD的交点 => P=A+r(B-A) => Px=Ax+r(Bx-Ax),Py=Ay+r(By-Ay)
- 如果(0≤r≤1)and(0≤s≤1) => AB、CD交点存在
- 如果(Bx-Ax)(Dy-Cy)-(By-Ay)(Dx-Cx)=0 => AB和CD平行
- 如果2成立,(Ay-Cy)(Dx-Cx)-(Ax-Cx)(Dy-Cx)也为0 => AB和CD共线
- 如果AB和CD相交,而交点不位于线段AB、CD之间,则交点位置可以通过以下条件判断
- r>1 => P位于AB的延长线上
- r<0 => P位于BA的延长线上
- s>1 => P位于CD的延长线上
- s<0 => P位于DC的延长线上
代码
bool IsIntersection(Point a,Point b,Point c,Point d) {
//AB = A + r(B-A), r 在[0,1]
//CD = C + t(D-C),s 在[0,1]
double r, s;
double deno = (b.X - a.X) * (d.Y - c.Y) - (b.Y - a.Y) * (d.X - c.X);
double mem1 = (a.Y - c.Y) * (d.X - c.X) - (a.X - c.X) * (d.Y - c.Y);
double mem2 = (a.Y - c.Y) * (b.X - a.X) - (a.X - c.X) * (b.Y - a.Y);
r = mem1 / deno;
s = mem2 / deno;
if (r > 1 || r < 0)
return false;
if (s > 1 || s < 0)
return false;
return true;
}
算法三:凸多边形
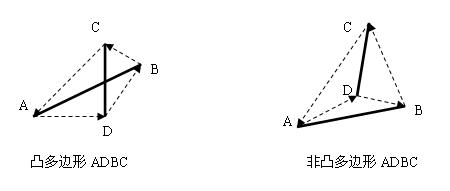
判断是否为凸多边形 –> 凸多边形 –> 线段相交
- 凸多边形:当从某个点开始绕一周,要么全顺时针拐弯,要么全逆时针
typedef struct vector{
double x,y;
}Vector; //向量
/*
* 由两个点构造一个向量
*/
Vector VectorConstruct(Point A, Point B) {
Vector v;
v.x = B.x - A.x;
v.y = B.y - A.y;
return v;
}
// 向量的叉积
double CrossProduct(Vector a, Vector b) {
return a.x * b.y - a.y * b.x;
}
/*
* 判断两线段(线段AB和CD)是否相交,是返回1,否0
* 判断四边形ACBD是否是一个凸四边形
*/
int SegmentIntersection(Point A, Point B, Point C, Point D) {
double c[4];
Vector AC = VectorConstruct(A, C);
Vector CB = VectorConstruct(C, B);
Vector BD = VectorConstruct(B, D);
Vector DA = VectorConstruct(D, A);
c[0] = CrossProduct(AC, CB);
c[1] = CrossProduct(CB, BD);
c[2] = CrossProduct(BD, DA);
c[3] = CrossProduct(DA, AC);
int f1=0, f2=0; // 计算正数,负数的个数
int i;
for (i=0; i<4; i++) {
if (c[i] > 0) f1++;
if (c[i] < 0) f2++;
}
if (f1 > 0 && f2 > 0) // 有正,有负,返回无交集
return 0;
else
return 1;
}
算法四:点在线的哪一侧
//功能:求点在有向直线左边还是右边
//返回:0共线、1左边、-1右边
int left_right(point a,point b,double x,double y) {
double t;
a.x -= x;
b.x -= x;
a.y -= y;
b.y -= y;
t = a.x*b.y-a.y*b.x;
return t==0 ? 0 : (t>0?1:-1); //注意:double类型t==0应该改成fabs(t)<10e-6
}
//功能:线段c,d和直线a,b是否相交
bool intersect1(point a,point b,point c,point d) {
return left_right(a,b,c.x,c.y)^left_right(a,b,d.x,d.y)==-2;
}
//功能:判断线段c,d和线段a,b是否相交
bool intersect(point a,point b,point c,point d) {
return intersect1(a,b,c,d) && intersect(c,d,a,b);
}
转载自:https://blog.csdn.net/summer_dew/article/details/82284311