地图处理方法-判断一个点是否在某个区域内
目录
判断一个点是否在某个区域内(多边形)
背景:
比如滴滴会根据乘客所在的不同区域,给出不同的价格。市区堵一点,那么价格也高点。获取服务范围只规定在某个范围内
原理:
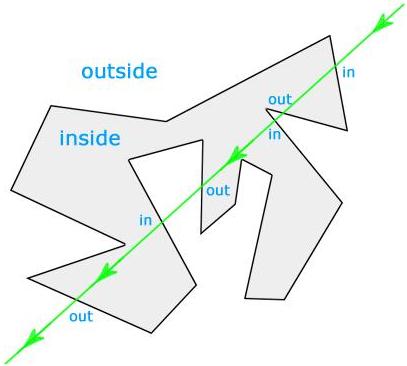
求解从该点向右发出的水平线射线与多边形各边的交点,当交点数为奇数,则在内部。
不过要注意几种特殊情况:1、点在边或者顶点上;2、点在边的延长线上;3、点出发的水平射线与多边形相交在顶点上
源代码:
Point类-多边形顶点的封装类如坐标(166.3,18.4)
Line类-多边形对应的各个边的封装类,如{(166.3,18.4), (166.9,19)}
MapUtil类-地图公共处理类
JAVA版本:
package com.qj.book.util;
/**
* Created by xsm48563 on 2017/10/31.
* 点
*/
public class Point {
/**
* 水平方向值/经度
*/
public Double X;
/**
* 垂直方向值/纬度
*/
public Double Y;
Point(Double x, Double y) {
x = x == null ? 0:x;
y = y == null ? 0:y;
this.X = x;
this.Y = y;
}
public boolean equals(Object obj) {
// 如果为同一对象的不同引用,则相同
if (this == obj) {
return true;
}
// 如果传入的对象为空,则返回false
if (obj == null) {
return false;
}
if (obj instanceof Point) {
Point point = (Point) obj;
if (point.X.equals(this.X) && point.Y.equals(this.Y)) {
return true;
} else {
return false;
}
} else {
return false;
}
}
public static void main(String[] args) {
Point A = new Point(1d, null);
Point B = new Point(null, 3d);
System.out.println(A.equals(B));
}
}
package com.qj.book.util;
import java.math.BigDecimal;
/**
* Created by xsm48563 on 2017/10/31.
* 线
*/
public class Line {
/**
* 端点1
*/
public Point POINTA;
/**
* 端点2
*/
public Point POINTB;
Line(Point pointA, Point pointB) {
this.POINTA = pointA;
this.POINTB = pointB;
}
/**
* 判断当前线段是否包含给定的点</br>
* 即给定的点是否在当前边上
* @param point
* @return
*/
public boolean isContainsPoint(Point point) {
boolean result = false;
//判断给定点point与端点1构成线段的斜率是否和当前线段的斜率相同
//给定点point与端点1构成线段的斜率k1
Double k1 = null;
if (point.X.equals(this.POINTA.X)) {
k1 = Double.NEGATIVE_INFINITY;
} else {
k1 = div(sub(point.Y, this.POINTA.Y), sub(point.X, this.POINTA.X));
}
//当前线段的斜率k2
Double k2 = null;
if (this.POINTB.X.equals(this.POINTA.X)) {
k2 = Double.NEGATIVE_INFINITY;
} else {
k2 = div(sub(this.POINTB.Y, this.POINTA.Y), sub(this.POINTB.X, this.POINTA.X));
}
if (k1 != null && k2 != null) {
if (k1.equals(k2)) {
//若斜率相同,继续判断给定点point的x是否在pointA.x和pointB.x之间,若在 则说明该点在当前边上
if (sub(point.X, this.POINTA.X) * sub(point.X, this.POINTB.X) < 0) {
result = true;
}
}
}
return result;
}
//叉积
double mult(Point a, Point b, Point c) {
return (a.X-c.X)*(b.Y-c.Y)-(b.X-c.X)*(a.Y-c.Y);
}
/**
* 给定线段是否与当前线段相交</br>
* 相交返回true, 不相交返回false
* @param line
* @return
*/
public boolean
isIntersect(Line line) {
Point aa = this.POINTA;
Point bb = this.POINTB;
Point cc = line.POINTA;
Point dd = line.POINTB;
if (Math.max(aa.X, bb.X) < Math.min(cc.X, dd.X)) {
return false;
}
if (Math.max(aa.Y, bb.Y) < Math.min(cc.Y, dd.Y)) {
return false;
}
if (Math.max(cc.X, dd.X) < Math.min(aa.X, bb.X)) {
return false;
}
if (Math.max(cc.Y, dd.Y) < Math.min(aa.Y, bb.Y)) {
return false;
}
if (mult(cc, bb, aa) * mult(bb, dd, aa) < 0 ) {
return false;
}
if ( mult(aa, dd, cc) * mult(dd, bb, cc) < 0 ) {
return false;
}
return true;
}
/**
* 提供精确的加法运算。
* @param v1 被加数
* @param v2 加数
* @return 两个参数的和
*/
public static double add(double v1,double v2){
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.add(b2).doubleValue();
}
/**
* 提供精确的减法运算。
* @param v1 被减数
* @param v2 减数
* @return 两个参数的差
*/
public static double sub(double v1,double v2){
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.subtract(b2).doubleValue();
}
/**
* 提供精确的乘法运算。
* @param v1 被乘数
* @param v2 乘数
* @return 两个参数的积
*/
public static double mul(double v1,double v2){
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.multiply(b2).doubleValue();
}
private static final int DEF_DIV_SCALE = 10;
/**
* 提供(相对)精确的除法运算,当发生除不尽的情况时,精确到
* 小数点以后10位,以后的数字四舍五入。
* @param v1 被除数
* @param v2 除数
* @return 两个参数的商
*/
public static double div(double v1,double v2){
return div(v1,v2,DEF_DIV_SCALE);
}
/**
* 提供(相对)精确的除法运算。当发生除不尽的情况时,由scale参数指
* 定精度,以后的数字四舍五入。
* @param v1 被除数
* @param v2 除数
* @param scale 表示表示需要精确到小数点以后几位。
* @return 两个参数的商
*/
public static double div(double v1,double v2,int scale){
if(scale<0){
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.divide(b2,scale,BigDecimal.ROUND_HALF_UP).doubleValue();
}
}
package com.qj.book.util;
import com.alibaba.fastjson.JSONArray;
import com.alibaba.fastjson.JSONObject;
import java.math.BigDecimal;
import java.util.ArrayList;
import java.util.List;
/**
* Created by xsm48563 on 2017/10/31.
* 图形专用类
*/
public class MapUtil {
/**
* 给定点和多边形,判断给定的点是否在多边形内
* @param point
* @param points
* @return
*/
public static boolean isPointInPolygon(Point point, List<Point> points) {
boolean result = false;
int intersectCount = 0;
// 判断依据:求解从该点向右发出的水平线射线与多边形各边的交点,当交点数为奇数,则在内部
//不过要注意几种特殊情况:1、点在边或者顶点上;2、点在边的延长线上;3、点出发的水平射线与多边形相交在顶点上
/**
* 具体步骤如下:
* 循环遍历各个线段:
* 1、判断点是否在当前边上(斜率相同,且该点的x值在两个端口的x值之间),若是则返回true
* 2、否则判断由该点发出的水平射线是否与当前边相交,若不相交则continue
* 3、若相交,则判断是否相交在顶点上(边的端点是否在给定点的水平右侧).若不在,则认为此次相交为穿越,交点数+1 并continue
* 4、若交在顶点上,则判断上一条边的另外一个端点与当前边的另外一个端点是否分布在水平射线的两侧.若是则认为此次相交为穿越,交点数+1.
*/
for (int i = 0; i < points.size(); i++) {
Point pointA = points.get(i);
Point pointB = null;
Point pointPre = null;
//若当前是第一个点,则上一点则是list里面的最后一个点
if (i == 0) {
pointPre = points.get(points.size() - 1);
} else {
pointPre = points.get(i - 1);
}
//若已经循环到最后一个点,则与之连接的是第一个点
if (i == (points.size() - 1)) {
pointB = points.get(0);
} else {
pointB = points.get(i + 1);
}
Line line = new Line(pointA, pointB);
//1、判断点是否在当前边上(斜率相同,且该点的x值在两个端口的x值之间),若是则返回true
boolean isAtLine = line.isContainsPoint(point);
if (isAtLine) {
return true;
} else {
//2、若不在边上,判断由该点发出的水平射线是否与当前边相交,若不相交则continue
//设置该射线的另外一个端点的x值=999,保证边的x永远不超过
Point radialPoint = new Point(999d, point.Y);
Line radial = new Line(point, radialPoint);
boolean isIntersect = radial.isIntersect(line);
if (!isIntersect) {
continue;
} else {
//3、若相交,则判断是否相交在顶点上(边的端点是否在给定点的水平右侧).若不在,则认为此次相交为穿越,交点数+1 并continue
if (!( (pointA.X > point.X) && (pointA.Y.equals(point.Y))
|| (pointB.X > point.X) && (pointB.Y.equals(point.Y)) )) {
intersectCount++;
continue;
} else {
//4、若交在顶点上,则判断上一条边的另外一个端点与当前边的另外一个端点是否分布在水平射线的两侧.若是则认为此次相交为穿越,交点数+1
if ((pointPre.Y - point.Y) * (pointB.Y - point.Y) < 0) {
intersectCount++;
}
}
}
}
}
result = intersectCount % 2 == 1;
return result;
}
public static void main(String[] args) {
Point point11 = new Point(1d, 2d);
Point point22 = new Point(2d, 4d);
Point point33 = new Point(3d, 4d);
Point point44 = new Point(5d, 2d);
Point point55 = new Point(5d, 1d);
Point point66 = new Point(3d, 0d);
List<Point> points = new ArrayList<>();
points.add(point11);
points.add(point22);
points.add(point33);
points.add(point44);
points.add(point55);
points.add(point66);
Point test = new Point(2d, 3d);
System.out.println(isPointInPolygon(test, points));
}
}
C++版本:
bool double_Equal(double num1, double num2)
{
if ((num1 - num2 > -0.0000001) && (num1 - num2 < 0.0000001))
return true;
else
return false;
}
class Point {
public:
//水平方向值/经度
double X;
//垂直方向值/纬度
double Y;
Point() = default;
Point(double x, double y) {
this->X = x;
this->Y = y;
}
bool equals(Point *obj) {
// 如果为同一对象的不同引用,则相同
if (this == obj) {
return true;
}
// 如果传入的对象为空,则返回false
if (obj == nullptr) {
return false;
}
Point point = *obj;
if ( double_Equal(point.X,this->X) && double_Equal(point.Y,this->Y) ) {
return true;
}
else {
return false;
}
}
};
class Line {
public:
//端点1
Point POINTA;
//端点2
Point POINTB;
Line(Point pointA, Point pointB) {
this->POINTA = pointA;
this->POINTB = pointB;
}
/**
* 判断当前线段是否包含给定的点</br>
* 即给定的点是否在当前边上
* @param point
* @return
*/
bool isContainsPoint(Point point) {
bool result = false;
//判断给定点point与端点1构成线段的斜率是否和当前线段的斜率相同
//给定点point与端点1构成线段的斜率k1
double k1 = 0;
bool needjudgment = true;
if (double_Equal(point.X,this->POINTA.X)) {
k1 = -DBL_MAX;
needjudgment = false;
}
else {
k1 = div(sub(point.Y, this->POINTA.Y), sub(point.X, this->POINTA.X));
}
//当前线段的斜率k2
double k2 = 0;
if ( double_Equal(this->POINTB.X,this->POINTA.X) ) {
k2 = -DBL_MAX;
needjudgment = false;
}
else {
k2 = div(sub(this->POINTB.Y, this->POINTA.Y), sub(this->POINTB.X, this->POINTA.X));
}
if (needjudgment == true) {
if (double_Equal(k1,k2)) {
//若斜率相同,继续判断给定点point的x是否在pointA.x和pointB.x之间,若在 则说明该点在当前边上
if (sub(point.X, this->POINTA.X) * sub(point.X, this->POINTB.X) < 0) {
result = true;
}
}
}
return result;
}
//叉积
double mult(Point a, Point b, Point c) {
return (a.X - c.X)*(b.Y - c.Y) - (b.X - c.X)*(a.Y - c.Y);
}
/**
* 给定线段是否与当前线段相交</br>
* 相交返回true, 不相交返回false
* @param line
* @return
*/
bool isIntersect(Line line) {
Point aa = this->POINTA;
Point bb = this->POINTB;
Point cc = line.POINTA;
Point dd = line.POINTB;
if (max(aa.X, bb.X) < min(cc.X, dd.X)) {
return false;
}
if (max(aa.Y, bb.Y) < min(cc.Y, dd.Y)) {
return false;
}
if (max(cc.X, dd.X) < min(aa.X, bb.X)) {
return false;
}
if (max(cc.Y, dd.Y) < min(aa.Y, bb.Y)) {
return false;
}
if (mult(cc, bb, aa) * mult(bb, dd, aa) < 0) {
return false;
}
if (mult(aa, dd, cc) * mult(dd, bb, cc) < 0) {
return false;
}
return true;
}
/**
* 提供精确的加法运算。 未完成版
* @param v1 被加数
* @param v2 加数
* @return 两个参数的和
*/
static double add(double v1, double v2) {
return v1+v2;
}
/**
* 提供精确的减法运算。 未完成版
* @param v1 被减数
* @param v2 减数
* @return 两个参数的差
*/
static double sub(double v1, double v2) {
return v1-v2;
}
/**
* 提供精确的乘法运算。 未完成版
* @param v1 被乘数
* @param v2 乘数
* @return 两个参数的积
*/
static double mul(double v1, double v2) {
return v1*v2;
}
/**
* 提供(相对)精确的除法运算,当发生除不尽的情况时,精确到
* 小数点以后10位,以后的数字四舍五入。 未完成版
* @param v1 被除数
* @param v2 除数
* @return 两个参数的商
*/
static double div(double v1, double v2) {
return v1 / v2;
}
};
/*
* 图形专用类
*/
class MapUtil {
/**
* 给定点和多边形,判断给定的点是否在多边形内
* @param point
* @param points
* @return
*/
public:
//多边形的各个点要是依次连接的输入的
static bool isPointInPolygon(Point point, vector<Point> points) {
bool result = false;
int intersectCount = 0;
// 判断依据:求解从该点向右发出的水平线射线与多边形各边的交点,当交点数为奇数,则在内部
//不过要注意几种特殊情况:1、点在边或者顶点上;2、点在边的延长线上;3、点出发的水平射线与多边形相交在顶点上
/**
* 具体步骤如下:
* 循环遍历各个线段:
* 1、判断点是否在当前边上(斜率相同,且该点的x值在两个端口的x值之间),若是则返回true
* 2、否则判断由该点发出的水平射线是否与当前边相交,若不相交则continue
* 3、若相交,则判断是否相交在顶点上(边的端点是否在给定点的水平右侧).若不在,则认为此次相交为穿越,交点数+1 并continue
* 4、若交在顶点上,则判断上一条边的另外一个端点与当前边的另外一个端点是否分布在水平射线的两侧.若是则认为此次相交为穿越,交点数+1.
*/
for (int i = 0; i < points.size(); i++) {
Point pointA = points.at(i);
Point pointB;
Point pointPre;
//若当前是第一个点,则上一点则是list里面的最后一个点
if (i == 0) {
pointPre = points.at(points.size() - 1);
}
else {
pointPre = points.at(i - 1);
}
//若已经循环到最后一个点,则与之连接的是第一个点
if (i == (points.size() - 1)) {
pointB = points.at(0);
}
else {
pointB = points.at(i + 1);
}
Line line = Line(pointA, pointB);
//1、判断点是否在当前边上(斜率相同,且该点的x值在两个端口的x值之间),若是则返回true
bool isAtLine = line.isContainsPoint(point);
if (isAtLine) {
return true;
}
else {
//2、若不在边上,判断由该点发出的水平射线是否与当前边相交,若不相交则continue
//设置该射线的另外一个端点的x值=999,保证边的x永远不超过
Point radialPoint = Point(180 , point.Y);
Line radial = Line(point, radialPoint);
//给定线段是否与当前线段相交 相交返回true
bool isIntersect = radial.isIntersect(line);
if (!isIntersect) {
continue;
}
else {
//3、若相交,则判断是否相交在顶点上(边的端点是否在给定点的水平右侧).若不在,则认为此次相交为穿越,交点数+1 并continue
if (!( (pointA.X > point.X) && (double_Equal(pointA.Y,point.Y))
|| (pointB.X > point.X) && (double_Equal(pointB.Y,point.Y)) )) {
intersectCount++;
continue;
}
else {
//4、若交在顶点上,则判断上一条边的另外一个端点与当前边的另外一个端点是否分布在水平射线的两侧.若是则认为此次相交为穿越,交点数+1
if ((pointPre.Y - point.Y) * (pointB.Y - point.Y) < 0) {
intersectCount++;
}
}
}
}
}
result = intersectCount % 2 == 1;
return result;
}
};
转载自:https://blog.csdn.net/qq_25800311/article/details/82917726